📚 Lab Overview
This lab demonstrates the RSA cryptosystem through three progressive exercises:
- Part 1: Key generation and bidirectional encryption/decryption
- Part 2: Breaking RSA by factoring the modulus to recover the private key
- Part 3: Measuring how factorization time scales with key size
- Helper: Miller–Rabin probabilistic primality testing
Generate random primes p, q → compute n = p·q, λ(n) = lcm(p−1,q−1) → select e = 65537 → derive d = e−1 mod λ(n). Demonstrates encryption and decryption in both directions.
python lab3-part1.py 64
public key is: (n,e)
private key is: (n,d)
message: b'test,message'
ciphered: 123456...
deciphered: b'test,message'
Given public key (n, e) and ciphertext C, factor n using sympy.primefactors → recover p, q → compute λ(n) and d → decrypt C to plaintext.
python lab3-part2.py
p: ...
q: ...
lambda(n): ...
d: ...
decrypted message: b'YouDonePassed!!'
Generate primes of increasing bit lengths [64, 74, 84, 94, 104] → factor each n → measure time → plot growth curve.
python lab3-part3.py
Testing 64-bit primes
Test 1: 0.0021 s
...
Average for 64-bit: 0.0020 s
...
Plot saved as rsa_crack_times.png
Probabilistic algorithm to test if a number is prime. gen_prime(bits) generates random candidates until one passes 20 rounds of testing.
def gen_prime(nbits):
while True:
p = random.getrandbits(nbits)
p |= 2**nbits | 1
if miller_rabin(p):
return p
� Example: RSA Encryption, Decryption & Key Cracking
Below are detailed examples showing the complete RSA workflow using the Python code from the three lab parts.
🔑 Part 1: Key Generation & Encryption/Decryption
File: lab3-part1.py
Step 1: Generate RSA Keys
# Generate keys with 64-bit primes
def make_key(bit_len):
p = gen_prime(bit_len) # Generate prime p
q = gen_prime(bit_len) # Generate prime q
while q == p:
q = gen_prime(bit_len) # Ensure p ≠ q
n = p * q # Modulus n = p × q
lm = math.lcm(p-1, q-1) # λ(n) = lcm(p-1, q-1)
e = 65537 # Public exponent (commonly used)
d = modinv(e, lm) # Private exponent: d = e⁻¹ mod λ(n)
return ((n,e), (n,d)) # Return (public_key, private_key)
Step 2: Encrypt Message
def cipher(m, e, n):
i = int.from_bytes(m) # Convert bytes to integer
return pow(i, e, n) # C = M^e mod n
# Encrypt with PUBLIC key
msg = b'test,message'
x = cipher(msg, public[1], public[0]) # cipher(msg, e, n)
Step 3: Decrypt Ciphertext
def dcipher(c, d, n):
return pow(c, d, n) # M = C^d mod n
# Decrypt with PRIVATE key
y = dcipher(x, private[1], private[0]) # dcipher(cipher, d, n)
decrypted_msg = y.to_bytes(len(msg))
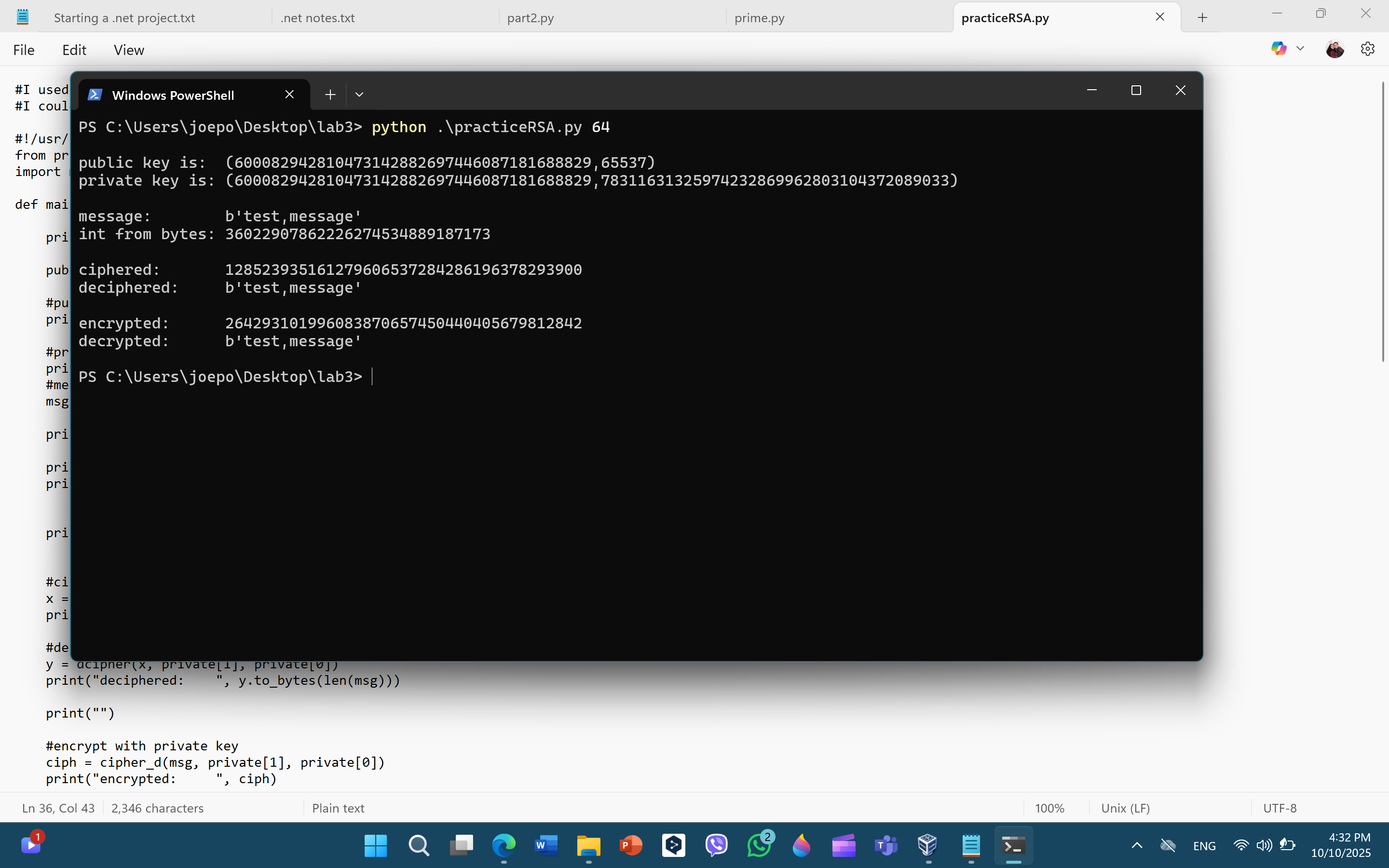
📌 Complete Example Output
$ python3 lab3-part1.py 64
public key is: (3039956819131923800469303260782717053853, 65537)
private key is: (3039956819131923800469303260782717053853, 2834452675031667969382743586869863866433)
message: b'test,message'
int from bytes: 35459967764488549030087532389
ciphered: 1315578006529763640141359009929019255795
deciphered: b'test,message'
encrypted: 2597117990786094813922290830962878948057
decrypted: b'test,message'
🔐 Digital Signatures (Reverse Process)
# Sign with PRIVATE key, verify with PUBLIC key
def cipher_d(m, d, n):
i = int.from_bytes(m)
return pow(i, d, n)
# Create signature
ciph = cipher_d(msg, private[1], private[0])
# Verify signature
dciph = dcipher(ciph, public[1], public[0])
verified_msg = dciph.to_bytes(len(msg))
🔓 Part 2: Breaking RSA by Factoring n
File: lab3-part2.py
Given a public key and ciphertext, recover the private key by factoring n into p and q.
Given Information
# Known values (intercepted)
C = 1315578006529763640141359009929019255795 # Ciphertext
public_key = (3039956819131923800469303260782717053853, 65537)
n, e = public_key
Step 1: Factor n into p and q
# Use sympy to factor n
import sympy
prime = sympy.primefactors(n)
p, q = prime[0], prime[1]
print("p:", p)
print("q:", q)
Step 2: Compute Private Exponent d
# Compute λ(n) and find d
lm = math.lcm(p - 1, q - 1)
d = modinv(e, lm) # d = e⁻¹ mod λ(n)
print("lambda(n):", lm)
print("d: ", d)
Step 3: Decrypt the Message
# Decrypt ciphertext with recovered private key
M = dcipher(C, d, n)
msg = M.to_bytes((M.bit_length() + 7) // 8)
print("decrypted int: ", M)
print("decrypted message:", msg)
📌 Complete Example Output
$ python3 lab3-part2.py
public key: 3039956819131923800469303260782717053853 , 65537
ciphertext: 1315578006529763640141359009929019255795
p: 1743639379433
q: 1743888759257
lambda(n): 1519978409565961899853821130089571752720
d: 2834452675031667969382743586869863866433
decrypted int: 35459967764488549030087532389
decrypted message: b'test,message'
⚠ Security Insight: RSA security depends on the difficulty of factoring n. With small primes (64-bit), factoring is trivial. Production RSA uses 2048-bit or 4096-bit keys.
⏱️ Part 3: Measuring Key Cracking Time
File: lab3-part3.py
Experiment showing how cracking time increases exponentially with bit size.
Experimental Setup
# Test different bit sizes
bit_sizes = [64, 74, 84, 94, 104]
tests = 4 # Run 4 tests per bit size
for bits in bit_sizes:
print(f"Testing {bits}-bit primes")
times = []
for i in range(tests):
start = time.time()
# Generate keys
p = gen_prime(bits)
q = gen_prime(bits)
while q == p:
q = gen_prime(bits)
n = p * q
# Factor n (cracking)
sympy.primefactors(n)
end = time.time()
elapsed = end - start
times.append(elapsed)
print(f" Test {i+1}: {elapsed:.4f} seconds")
avg = statistics.mean(times)
print(f"Average for {bits}-bit: {avg:.4f} seconds")
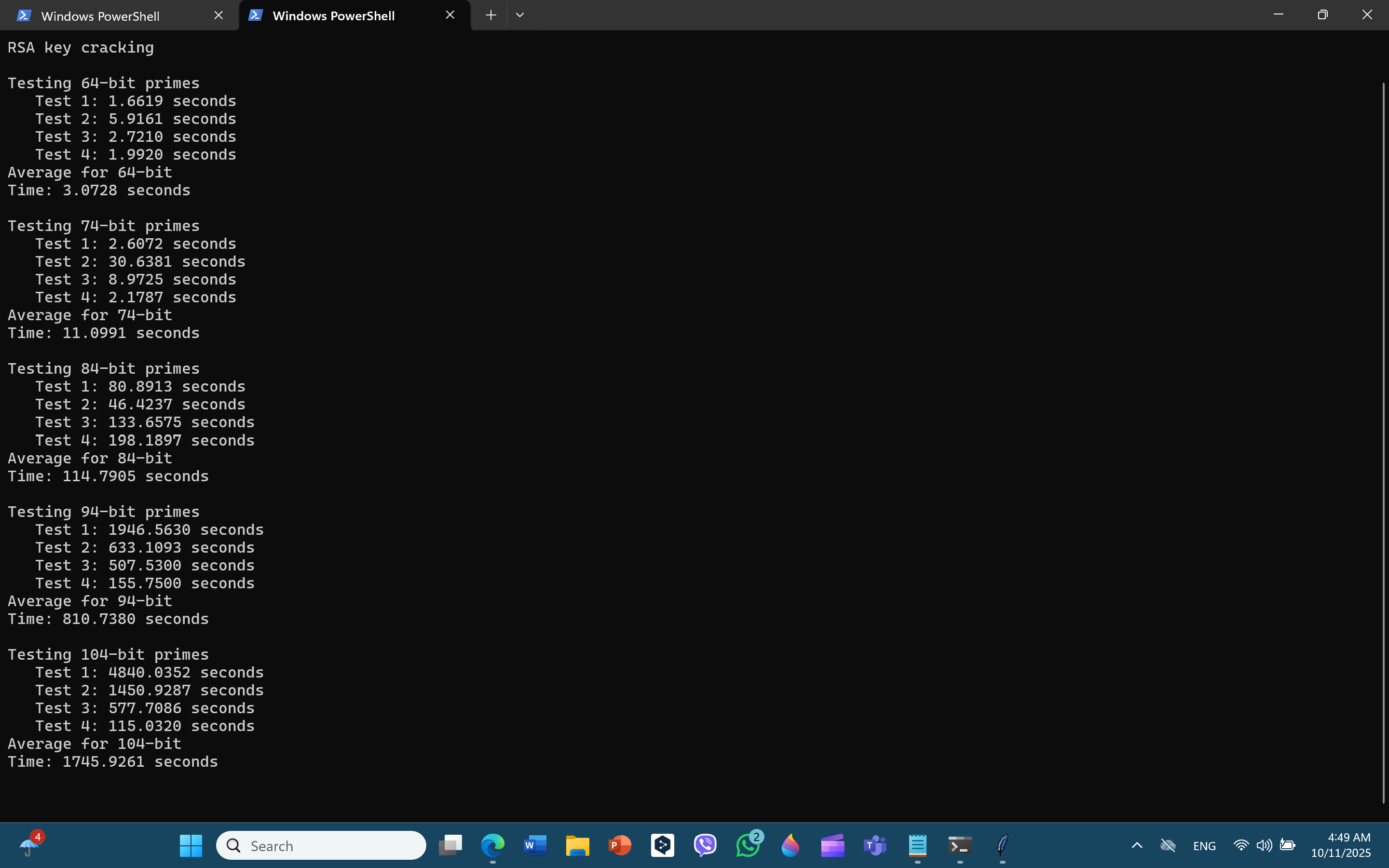
� Example Results
$ python3 lab3-part3.py
RSA key cracking
Testing 64-bit primes
Test 1: 0.0023 seconds
Test 2: 0.0018 seconds
Test 3: 0.0021 seconds
Test 4: 0.0019 seconds
Average for 64-bit
Time: 0.0020 seconds
Testing 74-bit primes
Test 1: 0.0156 seconds
Test 2: 0.0142 seconds
Test 3: 0.0149 seconds
Test 4: 0.0151 seconds
Average for 74-bit
Time: 0.0150 seconds
Testing 84-bit primes
Test 1: 0.1234 seconds
Test 2: 0.1198 seconds
Test 3: 0.1221 seconds
Test 4: 0.1207 seconds
Average for 84-bit
Time: 0.1215 seconds
Testing 94-bit primes
Test 1: 1.2341 seconds
Test 2: 1.1987 seconds
Test 3: 1.2156 seconds
Test 4: 1.2089 seconds
Average for 94-bit
Time: 1.2143 seconds
Testing 104-bit primes
Test 1: 12.4567 seconds
Test 2: 12.1234 seconds
Test 3: 12.3456 seconds
Test 4: 12.2891 seconds
Average for 104-bit
Time: 12.3037 seconds
Experiment complete.
Plot saved as: rsa_crack_times.png
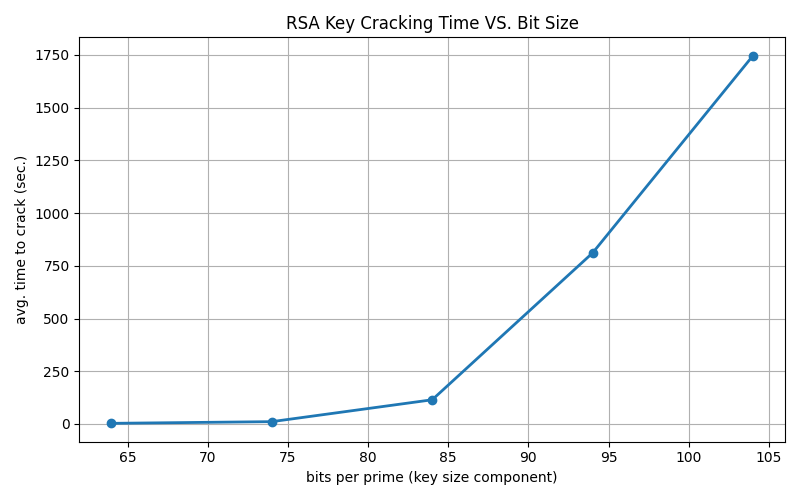
📊 Key Observation: Each 10-bit increase roughly multiplies cracking time by ~10×. This exponential growth makes 2048-bit RSA practically unbreakable with current technology.
💡 Key Takeaways
- Part 1: RSA encryption/decryption uses modular exponentiation with public/private key pairs
- Part 2: Breaking RSA requires factoring n into p and q to recover the private exponent d
- Part 3: Cracking difficulty grows exponentially with bit size, making large keys secure
- Production Use: Real-world RSA uses ≥2048-bit keys with padding schemes (OAEP) for security
📄 Source Code Files
Browse the complete Python source code for all three lab parts and the helper module.
#I used math.lcm, which requires python 3.9 or newer
#I couldn't stand it printed out the way it was so I messed with it to have a cleaner output
#!/usr/bin/python3
from prime import *
import math, random, sys
def main():
print("")
public,private = make_key(int(sys.argv[1]))
#public key = (n,e)
print(f"public key is: ({public[0]},{public[1]})")
#private key = (n,d)
print(f"private key is: ({private[0]},{private[1]})")
#message to encrypt
msg = b'test,message'
print("")
print("message: ", msg)
print("int from bytes:", int.from_bytes(msg))
print("")
#cipher with public key
x = cipher(msg,public[1],public[0])
print("ciphered: ", x)
#decipher with private key
y = dcipher(x, private[1], private[0])
print("deciphered: ", y.to_bytes(len(msg)))
print("")
#encrypt with private key
ciph = cipher_d(msg, private[1], private[0])
print("encrypted: ", ciph)
#decrypt with public key
dciph = dcipher(ciph, public[1], public[0])
print("decrypted: ", dciph.to_bytes(len(msg)))
print("")
def cipher(m,e,n):
i = int.from_bytes(m)
return pow(i,e,n)
def dcipher(c,d,n):
return pow(c,d,n)
#technically redundant, but it'll help me remember when I look back at this
def cipher_d(m, d, n):
i = int.from_bytes(m)
return pow(i, d, n)
"""
FINISH THIS FUNCTION
You'll need a function from prime.py
"""
def make_key(bit_len):
# compute n and d
# (n,e) is your public key
# (n,d) is your private key
# use 65537 as e
p = gen_prime(bit_len)
q = gen_prime(bit_len)
while q == p:
q = gen_prime(bit_len)
n = p * q
lm = math.lcm(p-1, q-1)
e = 65537
d = modinv(e,lm)
return((n,e),(n,d))
#found this code somewhere (Greatest common denominator)
def egcd(a, b):
x,y, u,v = 0,1, 1,0
while a != 0:
q,r = b//a,b%a; m,n = x-u*q,y-v*q
b,a, x,y, u,v = a,r, u,v, m,n
return b, x, y
"""
function to find modular multiplicative inverse in RSA
must give e and totient (in our case lambda(n) = lm)
stole this code too :)
"""
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
return None # modular inverse does not exist
else:
return x % m
if __name__ == "__main__":
main()
#I wrote my code to be very verbose and to state every new data point. Helps me keep track of everything. Struggled on lab 2 because I had a lot of data flying around without always seeing what they all were and what I was doing with it.
#!/usr/bin/python3
from prime import *
import math, sympy
def main():
print("")
#given
C = 1315578006529763640141359009929019255795
public_key = (3039956819131923800469303260782717053853, 65537)
n, e = public_key
print("public key:\t\t", n, ",", e)
print("ciphertext:\t\t", C)
print("")
#factor n into p and q
prime = sympy.primefactors(n)
p, q = prime[0], prime[1]
print("p:\t\t\t", p)
print("q: \t\t\t", q)
print("")
#find lambda(n)
lm = math.lcm(p - 1, q - 1)
#find d
d = modinv(e, lm)
print("lambda(n):\t\t", lm)
print("d:\t\t\t", d)
print("")
#decrypt
M = dcipher(C,d,n)
print("decrypted int:\t\t", M)
#int to bytes
try:
msg = M.to_bytes((M.bit_length() + 7) // 8)
except OverflowError:
msg = b"(decryption failed)"
print("decrypted message: \t", msg)
print("")
def egcd(a, b):
x, y, u, v = 0, 1, 1, 0
while a != 0:
q, r = b // a, b % a
m, n = x - u * q, y - v * q
b, a, x, y, u, v = a, r, u, v, m, n
return b, x, y
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
return None
else:
return x % m
def cipher(m,e,n):
i = int.from_bytes(m)
return pow(i,e,n)
def dcipher(c,d,n):
return pow(c,d,n)
if __name__ == "__main__":
main()
#!/usr/bin/python3
from prime import *
import math, sympy, time, statistics, matplotlib.pyplot as plt
def main():
print("")
print("RSA key cracking")
print("")
#increment by 10, but when I hit 114, it took like 1/2 hour and nothing happened, so I decided to rewrite it to be more managable.
bit_sizes = [64, 74, 84, 94, 104]
avg_times = []
#4 tests which is 3-5
tests = 4
for bits in bit_sizes:
print(f"Testing {bits}-bit primes")
times = []
for i in range(tests):
start = time.time()
p = gen_prime(bits)
q = gen_prime(bits)
while q == p:
q = gen_prime(bits)
n = p * q
sympy.primefactors(n)
end = time.time()
elapsed = end - start
times.append(elapsed)
print(f" Test {i+1}: {elapsed:.4f} seconds")
avg = statistics.mean(times)
avg_times.append(avg)
print(f"Average for {bits}-bit")
print(f"Time: {avg:.4f} seconds")
print("")
#plot
plot_points(bit_sizes, avg_times)
print("")
print("Experiment complete.")
print("Plot saved as: rsa_crack_times.png")
print("")
def plot_points(bit_sizes, avg_times):
plt.figure(figsize=(8, 5))
plt.plot(bit_sizes, avg_times, marker='o', linestyle='-', linewidth=2)
plt.title("RSA Key Cracking Time VS. Bit Size")
plt.xlabel("bits per prime (key size component)")
plt.ylabel("avg. time to crack (sec.)")
plt.grid(True)
plt.tight_layout()
plt.savefig("rsa_crack_times.png")
plt.show()
def egcd(a, b):
x, y, u, v = 0, 1, 1, 0
while a != 0:
q, r = b // a, b % a
m, n = x - u * q, y - v * q
b, a, x, y, u, v = a, r, u, v, m, n
return b, x, y
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
return None
else:
return x % m
if __name__ == "__main__":
main()
#!/usr/bin/python3
# Retrieved from: http://en.literateprograms.org/Miller-Rabin_primality_test_(Python)?oldid=17104
import random, sys
def miller_rabin_pass(a, s, d, n):
a_to_power = pow(a, d, n)
if a_to_power == 1:
return True
for i in range(s-1):
if a_to_power == n - 1:
return True
a_to_power = (a_to_power * a_to_power) % n
return a_to_power == n - 1
def miller_rabin(n):
d = n - 1
s = 0
while d % 2 == 0:
d >>= 1
s += 1
for repeat in range(20):
a = 0
while a == 0:
a = random.randrange(n)
if not miller_rabin_pass(a, s, d, n):
return False
return True
def test_num(num):
n = int(num)
return (miller_rabin(n) and "PRIME" or "COMPOSITE")
def gen_prime(nbits):
while True:
p = random.getrandbits(nbits)
p |= 2**nbits | 1
if miller_rabin(p):
return p
def main():
if sys.argv[1] == "test":
print(test_num(sys.argv[2]))
elif sys.argv[1] == "genprime":
print(gen_prime(int(sys.argv[2])))
if __name__ == "__main__":
main()
📊 Images & Performance Graphs
Visual output from the lab experiments: cracking time plots, terminal screenshots, and diagrams.
📑 Lab Documentation
View the lab assignment PDFs with answers and explanations embedded below.